


Next: 4 Henyey法
Up: 8 常微分方程式の数値解法:境界値問題
Previous: 2 境界値問題としてのLane-Emden 方程式
Subsections
境界値問題の例として、
恒星内部を記述する以下の方程式を現実的な仮定の下に解く事を考えよう。
基本方程式は、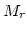 を独立変数に選べば、
を独立変数に選べば、
- 静水圧平衡
 |
(102) |
- 連続の式
 |
(103) |
- エネルギー保存式
 |
(104) |
- エネルギー輸達
 |
(105) |
但しここに
![\begin{displaymath}
\nabla \equiv
\min \left[
{{3}\over{16\pi acG}}{{\kappa L_r P}\over{M_r T^4}}, \nabla_{\rm ad} \right]
\end{displaymath}](img383.png) |
(106) |
で与えられる。これに、補助的な関係式
- 状態方程式
 |
(107) |
- 吸収係数
 |
(108) |
- 核反応生成率
 |
(109) |
を考慮する事によって、
(8.15) - (8.18)式は、
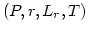 を変数とする四元連立常微分方程式となる。
これは
境界値問題で、
境界条件は
星の中心
を変数とする四元連立常微分方程式となる。
これは
境界値問題で、
境界条件は
星の中心 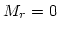 で
で
 |
(110) |
 |
(111) |
星の表面 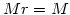 で
で
 |
(112) |
 |
(113) |
である。
恒星内部で両面の温度が 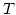 と
と 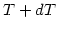 の層を考える。
この層に加わるネットの輻射圧を
の層を考える。
この層に加わるネットの輻射圧を 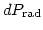 とする。
輻射平衡を考えると、
この輻射圧に伴う運動量は物質に吸収される。
今単位質量単位断面積
当たりの吸収係数を
とする。
輻射平衡を考えると、
この輻射圧に伴う運動量は物質に吸収される。
今単位質量単位断面積
当たりの吸収係数を 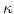 とすると、
単位面積単位時間当たり
とすると、
単位面積単位時間当たり 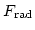 の輻射エネルギーが入射して
の輻射エネルギーが入射して 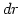 進む間に、
進む間に、
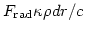 の運動量が吸収される。
従って、
の運動量が吸収される。
従って、
 |
(114) |
或いは
 |
(115) |
だから
 |
(116) |
を得る。
 |
(117) |
として
 |
(118) |
を得る。
静水圧平衡にある層で、bubble を 断熱的に 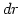 だけ平衡位置からずらせたとする。
最初の平衡位置における bubble の圧力と密度をそれぞれ
だけ平衡位置からずらせたとする。
最初の平衡位置における bubble の圧力と密度をそれぞれ
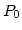 、
、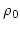 とする。これらは周囲の圧力、密度に等しい。
とする。これらは周囲の圧力、密度に等しい。
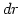 ずれた周囲の圧力、密度は
ずれた周囲の圧力、密度は
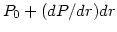 、
、
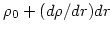 である。
ずれた位置での bubble の圧力
である。
ずれた位置での bubble の圧力 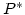 はその周囲の圧力に等しい。一方、密度
はその周囲の圧力に等しい。一方、密度
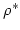 は
断熱変化により決まる。即ち
は
断熱変化により決まる。即ち
 |
(119) |
bubble が元の平衡位置に戻るかどうかは 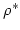 と周囲の密度の大小による。
戻るのが対流安定、どんどんずれていくのが対流不安定である。
従って、線形の範囲で、対流不安定の条件は
と周囲の密度の大小による。
戻るのが対流安定、どんどんずれていくのが対流不安定である。
従って、線形の範囲で、対流不安定の条件は
 |
(120) |
対流不安定の時、bubble の温度超過分は
単位質量当たりの熱エネルギー超過分はこれに 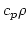 を掛けて与えられ、
単位面積単位時間当たりのエネルギーフラックスは更に速度を掛けたものである。
を掛けて与えられ、
単位面積単位時間当たりのエネルギーフラックスは更に速度を掛けたものである。
 |
(123) |
同様に密度超過分は
 |
(124) |
で与えられるが、移動によってなされる平均仕事量は
これに重力加速度と移動距離を掛けた上で平均したものである。これが運動エネルギー
の元であるから、
 |
(125) |
が成り立つ。
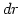 として、対流で混ざる代表的長さ
として、対流で混ざる代表的長さ 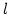 を採ると、エネルギーフラックスは
を採ると、エネルギーフラックスは
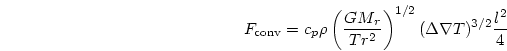 |
(126) |
で与えられる。
対流核の場合、温度超過は温度勾配に比べて無視出来るほど小さい。そこで
温度勾配は、
 |
(127) |
で与えられる。
微分方程式を解く前に、解のおおよその値に目星をつけよう。
基本方程式において、左辺の微分、例えば
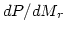 を単なる割り算
を単なる割り算 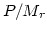 に置き換える。そのうえで
に置き換える。そのうえで
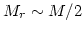 、
、
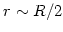 、
、
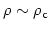 、
、
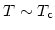 、
、
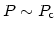 として恒星の物理諸量の大雑把な値を求めよ。
として恒星の物理諸量の大雑把な値を求めよ。
- 静水圧平衡
 |
(128) |
これより
 |
(129) |
- 連続の式
 |
(130) |
これより
 |
(131) |
- 状態方程式
ガス圧が主である場合を想定すると
 |
(132) |
これより
ただし
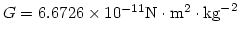 。
。
- エネルギー輸達
エネルギーは輻射によって運ばれていると想定すると
 |
(134) |
これより
今、太陽を想定して
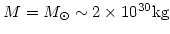 、
、
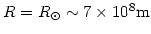 、
、
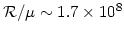 を代入すると
を代入すると
 |
(136) |
 |
(137) |
 |
(138) |
を得る。光度については、
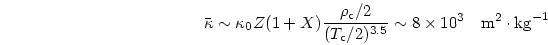 |
(139) |
だから
を得る。
 |
(141) |
 |
(142) |
 |
(143) |
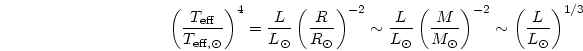 |
(144) |
輻射圧 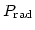 は
は
 |
(145) |
で与えられる。恒星の内部ではガス圧の他にこの輻射圧が無視できない。
温度の依存性がガス圧に比べて高いので、低密度高温状態ではむしろ輻射圧が主た
る圧力になる。
輻射圧の変化は
輻射輸達の方程式から
 |
(146) |
これから
これにより、輻射光度には或る上限値がある事が判る。即ち、
 |
(148) |
等号は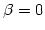 で成立するが、
で成立するが、
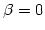 の場合は輻射圧だけで支える極限の場合である。
の場合は輻射圧だけで支える極限の場合である。
星の光度は質量の何乗ぐらいで変わっているだろうか? 星の質量と光度の関係を
導いてみよう。
臨界光度に近い高温大質量星の場合、
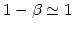 ゆえ
ゆえ
 |
(149) |
となり、
光度は星の質量の1乗に比例する。
一方ガス圧が主になる中質量星、低質量星では、前に導いたように、
 |
(150) |
となり、吸収係数に依存する。中質量星の場合には吸収係数としては
電子散乱が主たる寄与をしており、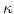 は 温度によらない。
従って、光度は星の質量の3乗に比例する。
一方、低質量星では 吸収係数へは Kramers の項の寄与が大きい。
そこで
は 温度によらない。
従って、光度は星の質量の3乗に比例する。
一方、低質量星では 吸収係数へは Kramers の項の寄与が大きい。
そこで
よって
 |
(152) |
となり、
光度は星の質量の5.5乗に比例する。
恒星内部を記述する
4本の
微分方程式を、中心及び表面でのそれぞれ2本ずつ計4本の境界条件とともに、数値
的に解く。
中心と表面からそれぞれ数値積分をはじめ、ある適当な所で両者が
フィットするように
する。
星の中心から外に向かって
積分していくとしたら二つの物理量
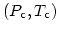 がパラメーターとして残る。
星の表面から内に向かって
積分していくとしたら二つの物理量
がパラメーターとして残る。
星の表面から内に向かって
積分していくとしたら二つの物理量 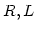 がパラメーターとして残る。
解がフィットするようなパラメーター
がパラメーターとして残る。
解がフィットするようなパラメーター
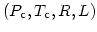 を捜す事になる。
を捜す事になる。
星としては 2 - 15 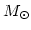 の主系列星を考えることにしよう。
そこで
状態方程式としては理想気体と輻射を考えて
の主系列星を考えることにしよう。
そこで
状態方程式としては理想気体と輻射を考えて
ここに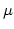 は
は
 |
(154) |
で、平均分子量。また
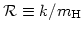 で、
で、
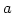 は
は
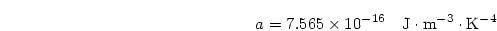 |
(155) |
で radiation constant。
吸収係数としては
Kramers + 電子散乱 を考え
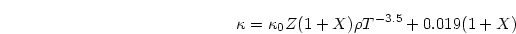 |
(156) |
 |
(157) |
とする。
核反応生成率は
CNO-cycle を考え
 |
(158) |
 |
(159) |
とする。
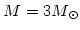 、
、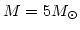 、
、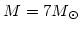 、
、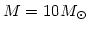 の星の Zero-Age Main-Sequence 時のモデルを計算してみよう。
星が Zero-Age Main-Sequence に達した時は、それに先立つ林-フェーズにおける
星全体に及ぶ対流の結果、化学組成は一様になっていると考えられる。
そこで化学組成一様な星のモデルを計算する。
の星の Zero-Age Main-Sequence 時のモデルを計算してみよう。
星が Zero-Age Main-Sequence に達した時は、それに先立つ林-フェーズにおける
星全体に及ぶ対流の結果、化学組成は一様になっていると考えられる。
そこで化学組成一様な星のモデルを計算する。
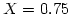 ,
, 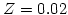 としよう。
最初のステップとして中心からの積分を行う。
二つの物理量
としよう。
最初のステップとして中心からの積分を行う。
二つの物理量
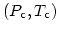 がパラメーターとして残る。
積分は Runge-Kutta 法で行う。
中心近傍での物理量は
がパラメーターとして残る。
積分は Runge-Kutta 法で行う。
中心近傍での物理量は
 |
(160) |
 |
(161) |
 |
(162) |
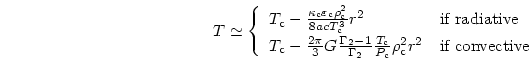 |
(163) |
パラメーター
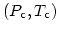 の現実的な値としては、
前回計算を行ったポリトロープ球から得られる値を用いると良いだろう。
(後で行う表面からの積分の解と fitting point で解が
フィットするようなパラメーターを捜さなければならないので、パラメーターを任意
に変えられるようなプログラムを書く必要がある
の現実的な値としては、
前回計算を行ったポリトロープ球から得られる値を用いると良いだろう。
(後で行う表面からの積分の解と fitting point で解が
フィットするようなパラメーターを捜さなければならないので、パラメーターを任意
に変えられるようなプログラムを書く必要がある
![[*]](footnote.png) 。)
。)
中心近傍での解の振舞を議論せよ。
次のステップとして表面からの積分を行う。
二つの物理量 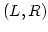 がパラメーターとして残る。独立変数として
がパラメーターとして残る。独立変数として 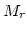 を用いるのが良いだろう。
積分は 前回同様 Runge-Kutta 法で行う。
を用いるのが良いだろう。
積分は 前回同様 Runge-Kutta 法で行う。
今考えているような
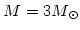 、
、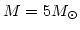 、
、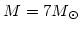 、
、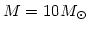 の星では、エ
ネルギーは中心近傍では対流で運ばれ、外側では輻射で運ばれる。
そこで radiative envelope を考える。
すると
の星では、エ
ネルギーは中心近傍では対流で運ばれ、外側では輻射で運ばれる。
そこで radiative envelope を考える。
すると
 |
(164) |
だが、表面近傍では
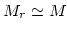
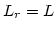 なので、上の式は
なので、上の式は
 |
(165) |
となる。ここで opacity を
 |
(166) |
とすると、上の式は更に
 |
(167) |
となるから、
この式を積分して
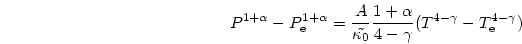 |
(168) |
を得る。但し、ここで
 |
(169) |
であり、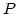 、
、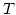 の表面での値をそれぞれ
の表面での値をそれぞれ 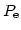 、
、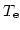 とした。
もし
とした。
もし 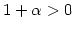 且つ
且つ 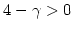 であれば、上記
であれば、上記 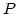 -
-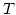 関係は
表面での値
関係は
表面での値 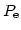 、
、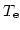 に殆ど依存しなくなる。
実際 Kramers' opacity では
に殆ど依存しなくなる。
実際 Kramers' opacity では 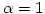 、
、 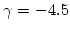 でこの条件を満たす。
そこで、ここでは、星の表面 (
でこの条件を満たす。
そこで、ここでは、星の表面 (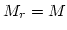 )では
)では
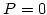 、
、 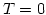 とする。
Kramers' opacity を採用すると、
とする。
Kramers' opacity を採用すると、
 |
(170) |
となる。そこで表面領域では
解くべき方程式は
 |
(171) |
 |
(172) |
 |
(173) |
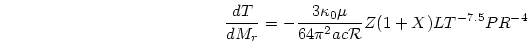 |
(174) |
となる。
これらを 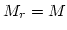 から内側に積分していく。
初期値として、
から内側に積分していく。
初期値として、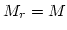 で
で 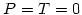 。そこでの
。そこでの 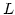 及び
及び 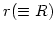 が
二つの自由パラメーターになる。
が
二つの自由パラメーターになる。
パラメーター 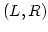 の現実的な値としては、
ポリトロープ球から得られる値を用いると良いだろう。
(いずれにせよ、前回行った中心からの積分の解と fitting point で解が
フィットするようなパラメーターを捜さなければならないので、パラメーターを任意
に変えられるようなプログラムを書く必要がある
の現実的な値としては、
ポリトロープ球から得られる値を用いると良いだろう。
(いずれにせよ、前回行った中心からの積分の解と fitting point で解が
フィットするようなパラメーターを捜さなければならないので、パラメーターを任意
に変えられるようなプログラムを書く必要がある
![[*]](footnote.png) 。)
。)
表面近傍では温度は
 |
(175) |
で良く近似できる事を導け。
中心と表面からそれぞれ数値積分をはじめ、ある適当な所で両者が
フィットするようにする。
中心からの積分は
二つの物理量
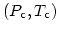 をパラメーターとして行った。
この時、
ある適当なフィッティングポイント
をパラメーターとして行った。
この時、
ある適当なフィッティングポイント 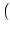 例えば
例えば 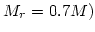 での
4変数の値
での
4変数の値
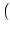 これらを
これらを
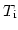 ,
,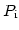 ,
,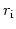 ,
,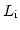 と記そう。
と記そう。 は
は
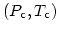 の関数になっている。
の関数になっている。
 |
(176) |
 |
(177) |
 |
(178) |
 |
(179) |
同様にして、
ある適当なフィッティングポイント  例えば
例えば 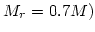 での
表面から積分してきた
4変数
での
表面から積分してきた
4変数
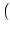 これらを
これらを
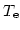 ,
,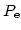 ,
,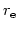 ,
,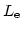 と記そう。
と記そう。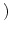 の値は
の値は 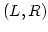 の関数になっている。
の関数になっている。
 |
(180) |
 |
(181) |
 |
(182) |
 |
(183) |
両者が一致する必要が条件は
 |
(184) |
 |
(185) |
 |
(186) |
 |
(187) |
だが、任意に選んだ
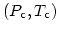 ,
, 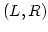 に対してはこの条件は満たされない。この条件を満たす
に対してはこの条件は満たされない。この条件を満たす
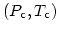 ,
, 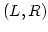 を
を
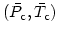 ,
,
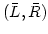 とし、その時の
フィティングポイントでの
とし、その時の
フィティングポイントでの 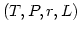 の値を
の値を
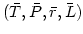 とし、
前に用いた
とし、
前に用いた
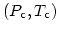 ,
, 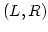 との差を
との差を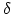 で表わすことにする。
今、
前に用いた
で表わすことにする。
今、
前に用いた
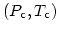 ,
, 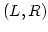 がかなり
がかなり
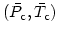 ,
,
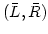 に近いとすると、
フィティングの条件は、
に近いとすると、
フィティングの条件は、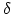 の一次の範囲では
の一次の範囲では
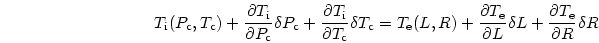 |
(188) |
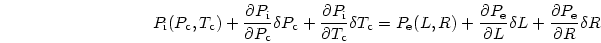 |
(189) |
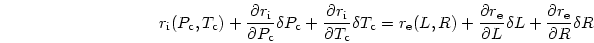 |
(190) |
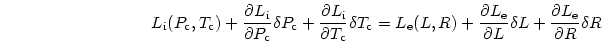 |
(191) |
となる。
ここで微分係数
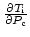 などは、フィティングポイント
での
などは、フィティングポイント
での 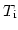 の値のパラメーター
の値のパラメーター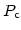 に対する依存性で、これらは
数値的に調べる事が出来る。従って、上の4本の式は、
に対する依存性で、これらは
数値的に調べる事が出来る。従って、上の4本の式は、
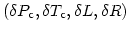 を4つの未知変数とする代数方程式と見做す事が出来る
を4つの未知変数とする代数方程式と見做す事が出来る
![[*]](footnote.png) 。
。
これを解いて最初に用いたパラメーター
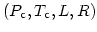 に対する補正量
に対する補正量
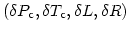 を求める。このプロセスを繰り返し、収束するまで行えば
フィティングする解が求められた事になる。
を求める。このプロセスを繰り返し、収束するまで行えば
フィティングする解が求められた事になる。



Next: 4 Henyey法
Up: 8 常微分方程式の数値解法:境界値問題
Previous: 2 境界値問題としてのLane-Emden 方程式
Jun Makino
平成15年4月17日
![]() と
と ![]() の層を考える。
この層に加わるネットの輻射圧を
の層を考える。
この層に加わるネットの輻射圧を ![]() とする。
輻射平衡を考えると、
この輻射圧に伴う運動量は物質に吸収される。
今単位質量単位断面積
当たりの吸収係数を
とする。
輻射平衡を考えると、
この輻射圧に伴う運動量は物質に吸収される。
今単位質量単位断面積
当たりの吸収係数を ![]() とすると、
単位面積単位時間当たり
とすると、
単位面積単位時間当たり ![]() の輻射エネルギーが入射して
の輻射エネルギーが入射して ![]() 進む間に、
進む間に、
![]() の運動量が吸収される。
従って、
の運動量が吸収される。
従って、
![]() だけ平衡位置からずらせたとする。
最初の平衡位置における bubble の圧力と密度をそれぞれ
だけ平衡位置からずらせたとする。
最初の平衡位置における bubble の圧力と密度をそれぞれ
![]() 、
、![]() とする。これらは周囲の圧力、密度に等しい。
とする。これらは周囲の圧力、密度に等しい。
![]() ずれた周囲の圧力、密度は
ずれた周囲の圧力、密度は
![]() 、
、
![]() である。
ずれた位置での bubble の圧力
である。
ずれた位置での bubble の圧力 ![]() はその周囲の圧力に等しい。一方、密度
はその周囲の圧力に等しい。一方、密度
![]() は
断熱変化により決まる。即ち
は
断熱変化により決まる。即ち
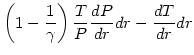
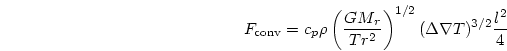
![]() を単なる割り算
を単なる割り算 ![]() に置き換える。そのうえで
に置き換える。そのうえで
![]() 、
、
![]() 、
、
![]() 、
、
![]() 、
、
![]() として恒星の物理諸量の大雑把な値を求めよ。
として恒星の物理諸量の大雑把な値を求めよ。
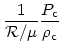
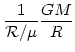
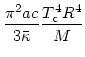
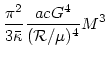
![]() 、
、
![]() 、
、
![]() を代入すると
を代入すると
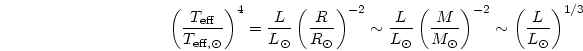
![]() は
は
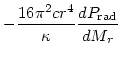
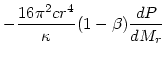
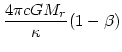
![]() ゆえ
ゆえ
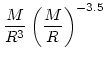
![]() の主系列星を考えることにしよう。
そこで
状態方程式としては理想気体と輻射を考えて
の主系列星を考えることにしよう。
そこで
状態方程式としては理想気体と輻射を考えて
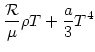
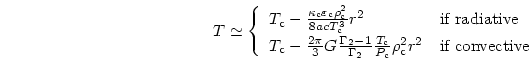
![]() の現実的な値としては、
前回計算を行ったポリトロープ球から得られる値を用いると良いだろう。
(後で行う表面からの積分の解と fitting point で解が
フィットするようなパラメーターを捜さなければならないので、パラメーターを任意
に変えられるようなプログラムを書く必要がある
の現実的な値としては、
前回計算を行ったポリトロープ球から得られる値を用いると良いだろう。
(後で行う表面からの積分の解と fitting point で解が
フィットするようなパラメーターを捜さなければならないので、パラメーターを任意
に変えられるようなプログラムを書く必要がある
![[*]](footnote.png) 。)
。)
![]() 、
、![]() 、
、![]() 、
、![]() の星では、エ
ネルギーは中心近傍では対流で運ばれ、外側では輻射で運ばれる。
そこで radiative envelope を考える。
すると
の星では、エ
ネルギーは中心近傍では対流で運ばれ、外側では輻射で運ばれる。
そこで radiative envelope を考える。
すると
![]() の現実的な値としては、
ポリトロープ球から得られる値を用いると良いだろう。
(いずれにせよ、前回行った中心からの積分の解と fitting point で解が
フィットするようなパラメーターを捜さなければならないので、パラメーターを任意
に変えられるようなプログラムを書く必要がある
の現実的な値としては、
ポリトロープ球から得られる値を用いると良いだろう。
(いずれにせよ、前回行った中心からの積分の解と fitting point で解が
フィットするようなパラメーターを捜さなければならないので、パラメーターを任意
に変えられるようなプログラムを書く必要がある
![[*]](footnote.png) 。)
。)
![]() 例えば
例えば ![]() での
表面から積分してきた
4変数
での
表面から積分してきた
4変数
![]() これらを
これらを
![]() ,
,![]() ,
,![]() ,
,![]() と記そう。
と記そう。![]() の値は
の値は ![]() の関数になっている。
の関数になっている。
![[*]](footnote.png) 。
。
![]() に対する補正量
に対する補正量
![]() を求める。このプロセスを繰り返し、収束するまで行えば
フィティングする解が求められた事になる。
を求める。このプロセスを繰り返し、収束するまで行えば
フィティングする解が求められた事になる。