

次へ: 3 臨界点
上へ: 天文学特別講義IV
戻る: 1 ジーンズ不安定
Subsections
恒星系の場合を考えることにしよう。
何度も出てきたがもう一回式を書いておく。
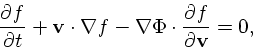 |
(15) |
ここで 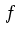 は6次元位相空間での分布関数である。
は6次元位相空間での分布関数である。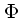 は重力ポテンシャ
ルであり、以下のポアソン方程式の解として与えられる。
は重力ポテンシャ
ルであり、以下のポアソン方程式の解として与えられる。
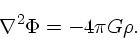 |
(16) |
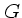 は重力定数であり、
は重力定数であり、 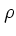 は空間での質量密度
は空間での質量密度
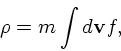 |
(17) |
である。
これを流体の時と同様に線形化して、その振舞いを調べる。分布関数を 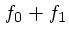 、ポテンシャルを
、ポテンシャルを
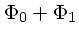 とし、添字0がつくほうは定常解で
あるとして式を整理すれば
とし、添字0がつくほうは定常解で
あるとして式を整理すれば
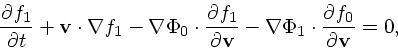 |
(18) |
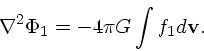 |
(19) |
ということになる。これが線形化された無衝突ボルツマン方程式である。
上の線形化されたボルツマン方程式は、平衡解の回りならば何でも使えるが、
ここではもっとも簡単に解析できる場合として空間分布が一様な場合を考える。
これから 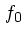 は速度だけの関数であり、
は速度だけの関数であり、 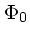 は定数としていいことに
なるので
は定数としていいことに
なるので
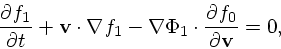 |
(20) |
と少し式が簡単になる。まず、流体の場合と同じような平面波型の解を考えて
みよう。
速度空間の方にも伝わっていく波とかいうのも考えられないわけではないが、
とりあえずそういうのは考えない。これらを上の線形化した式に入れれば
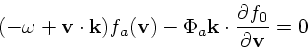 |
(23) |
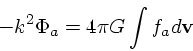 |
(24) |
となる。これらから 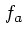 を消せば、
を消せば、 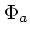 も落ちて
も落ちて
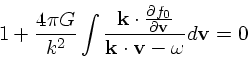 |
(25) |
となって、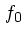 が与えられていれば
が与えられていれば 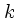 と
と 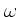 の関係、すなわち分散
関係を与える。
の関係、すなわち分散
関係を与える。
もっとも、これはちょっと困った式で、
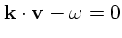 が特
異点になっている。したがって、実数の振動数を考えるのはすこし厄介な話に
なる。まず、臨界点、すなわち振動数が
が特
異点になっている。したがって、実数の振動数を考えるのはすこし厄介な話に
なる。まず、臨界点、すなわち振動数が 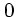 の場合と、不安定、すなわち振動
数が純虚数の場合を考えよう。
の場合と、不安定、すなわち振動
数が純虚数の場合を考えよう。


次へ: 3 臨界点
上へ: 天文学特別講義IV
戻る: 1 ジーンズ不安定
Jun Makino
平成21年5月25日
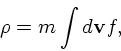
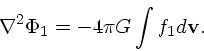
![]() は速度だけの関数であり、
は速度だけの関数であり、 ![]() は定数としていいことに
なるので
は定数としていいことに
なるので
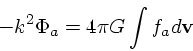
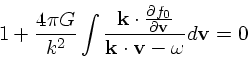
![]() が特
異点になっている。したがって、実数の振動数を考えるのはすこし厄介な話に
なる。まず、臨界点、すなわち振動数が
が特
異点になっている。したがって、実数の振動数を考えるのはすこし厄介な話に
なる。まず、臨界点、すなわち振動数が ![]() の場合と、不安定、すなわち振動
数が純虚数の場合を考えよう。
の場合と、不安定、すなわち振動
数が純虚数の場合を考えよう。